Our Team
Long Wang
Biomedical engineer
Dr. Wang’s research interests are multidisciplinary and lie at the intersection of structural engineering, material science, and data analytics. Specifically, Dr. Wang’s research centers on developing robust multifunctional material-based sensing systems and data-driven diagnostic and prognostic techniques for assessing structural performance and human health. Dr. Wang is passionate about promoting research experiences for diverse groups of high school students, undergraduate students, and graduate students through participation in hands-on experimental and computational research.
Max Lewter
Biomedical engineer
Max Lewter is a third year Biomedical Engineering student concentrating in Bioinstrumentation at California Polytechnic State University, SLO. His interests lie at the intersection of biomedical electrical design and programming as he pursues a minor in Computer Science. This project was an excellent opportunity to get relevant experience in the research field and for connecting with fellow students and faculty.
Josh Rizzolo
Electrical Engineer
Joshua Rizzolo is a fourth-year Electrical Engineering student at California Polytechnic State University SLO. He is committed to helping new students adjust to their life at college through the New Student and Transition Program. He is also curious about technological advancements in the fields of photovoltaics, energy storage, and medical imaging, hoping to enter the workforce in one of these fields after graduation.
Acknowledgements
We appreciate the support to our research project graciously provided by Northrop Grumman Foundation and the Summer Undergraduate Program (SURP) at the Cal Poly College of Engineering.
Inverse Problem Solving for an Electrical Imaging Technique
Problem Statement
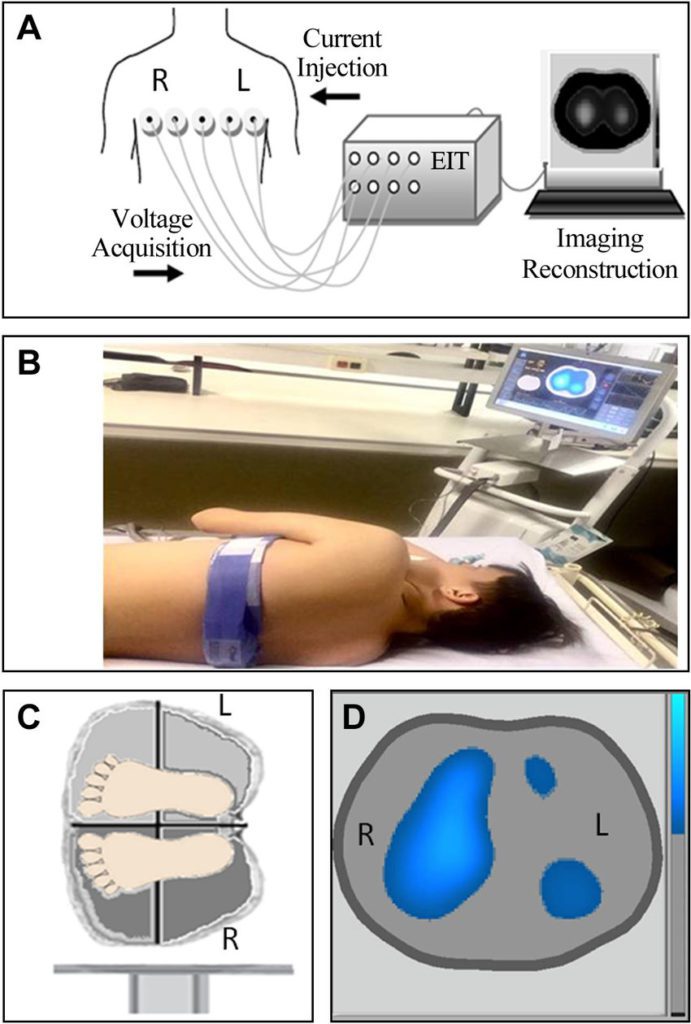
Electrical impedance tomography (EIT) provides a safe and quick way to image various bodies but comes at the cost of low-spatial resolution. The ill-posed inverse problem is computationally difficult and has prohibited widespread use of EIT in the medical world.
Introduction
Electrical Impedance Tomography (EIT) is an imaging technique that uses voltage and current information to reconstruct an estimation of the conductivity distribution of a body.
The EIT problem is often broken down into two parts, the forward problem, and the inverse problem. The forward problem involves using an estimated conductivity distribution to solve for the voltages and has a unique solution. The ill-posed inverse problem involves estimating the conductivity distribution from voltage data and allows for reconstruction of internal elements in the body. Developing an algorithm to solve the inverse problem has been the focus of this project and to do this, a Bayesian approach is used. The Bayesian approach is powerful because:
- It incorporates prior information
- Allows for error estimation
- Makes reasonable estimations from small amounts of data
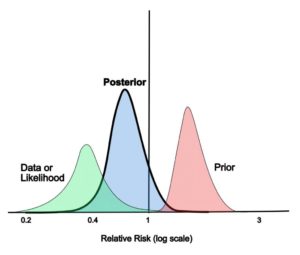
As seen above, Bayesian statistics incorporates prior information as well as data in order to create a posterior distribution. We attempted two different Bayesian approaches, the Bayesian Inference model and the Structure-Aware Sparse Bayesian Learning model.
Methods
Bayesian Inference Model
In this project, we first use EIDORS, a MATLAB library designed specifically to solve the EIT problem, to solve for the Jacobian matrix (a matrix of partial derivatives) and initial voltages. Then, utilizing python code and pymc3’s Bayesian tools, we can create a likelihood function (l), a prior distribution (p), and a posterior distribution.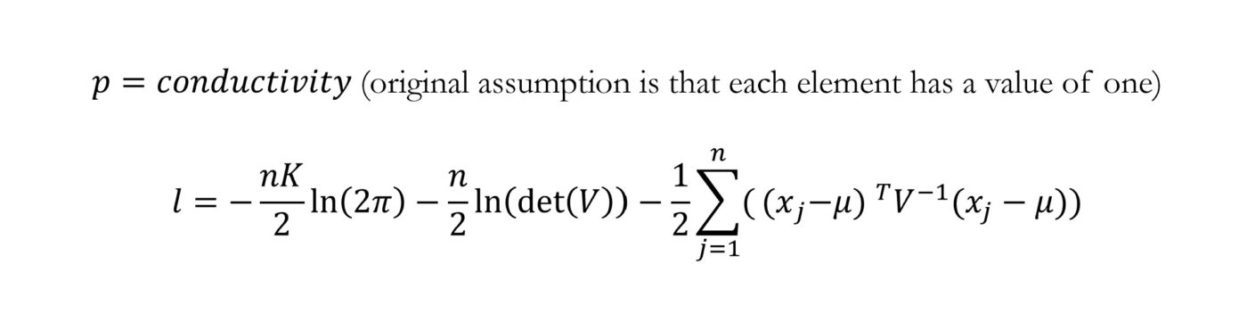
Sampling from this posterior distribution yields potential conductivity distributions, which can be run through the forward solver and checked against the initial voltages. The forward solver is:
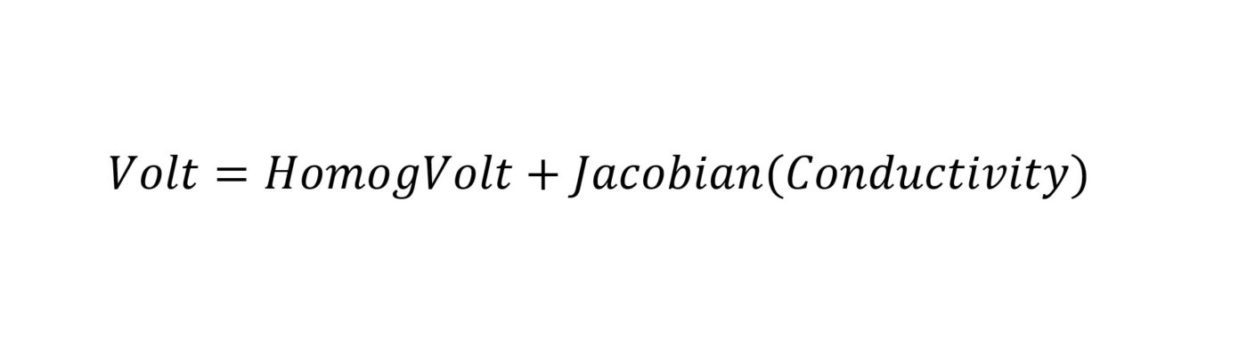This comparison is not particularly computationally expensive and thus can help to confirm a good estimation. Finally, Images can be reconstructed in EIDORS based off the estimated conductivity field.
Structure-Aware Sparse Bayesian Learning Model
Bayesian statistics encouraging the inclusion of prior information is powerful for EIT. While there is often little prior information known, the context of EIT it is known that most bodies take on a clustered-sparse structure. This means that, using difference EIT to subtract out background conductivity, there are few non-zero entries in the discrete conductivity distribution of the body; these entries also typically come in clusters (e.g., organs in a chest cavity). This knowledge allows the selection of a prior distribution that suppresses lone non-zero entries and promotes sharp edges to more accurately model the structure of bodies to be imaged.
Unlike similar approaches, Structure-Aware Sparse Bayesian Learning (SA SBL) does not require information about size, location, or number of clusters. Instead, the algorithm promotes the existence of clusters of non-zero entries allowing it to automatically explore the distribution. This exploration requires the inclusion of three hyperparameters (parameters of the prior distribution) with complex learning rules. But the process can still be done algorithmically.
Images
Bayesian Inference Method
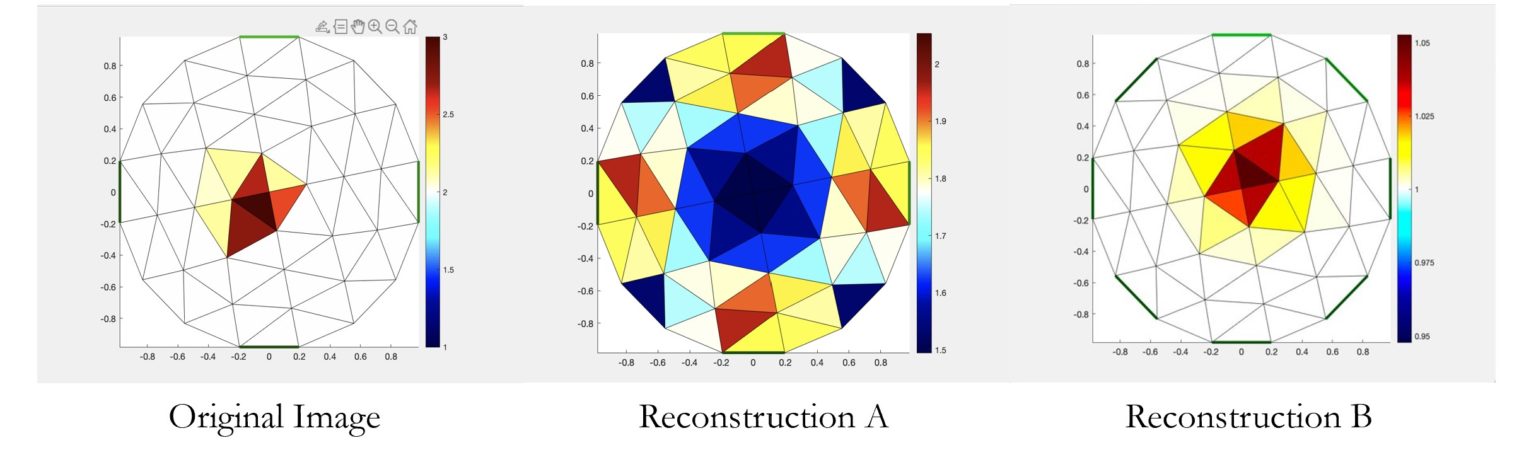
In reconstruction attempts, on average, nine out of ten attempts yields reconstruction A and one out of ten attempts yields reconstruction B. The results are unstable, but future steps will be taken to stabilize and focus the reconstructions.
SA-SBL Method
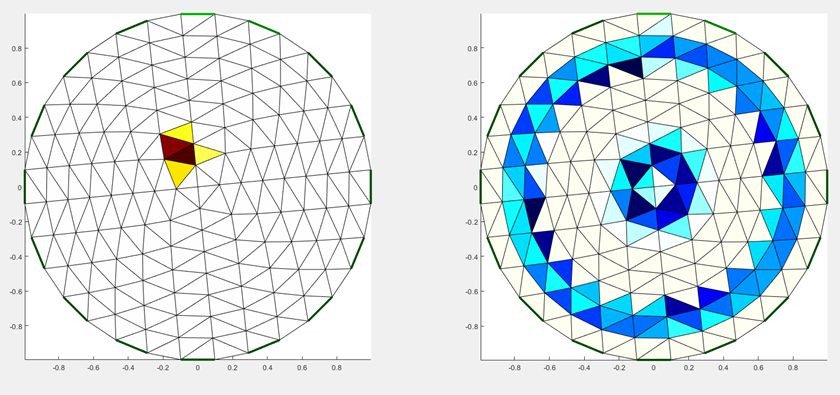
Every single reconstruction attempt with this algorithm produces two concentric rings of low conductivity. We have changed the mesh shape and number of elements, as well as the location, size, and shape of the anomaly to little effect.
This project is sponsored by Northrop Grumman
Future Steps
To create an accurate image, further experiments must be done to try to adjust the problems in the algorithms. Specifically, in the Bayesian Inference Method:
- adjustments to the covariance of the multivariate normal curve
- More experimentation with pymc3 functions regarding the setup of the posterior distribution
- Further improvement of the gradient based sampling system
- Plot Convergence of Reconstruction Algorithm
- Implement difference EIT
- Examine each formula translated into Matlab for errors
- Test with multiple anomalies
- Test with negative conductivity anomalies
- Implement mesh with square elements (as below)
Conclusion
With the guidance of our advisor we were able to make strides towards achieving a more efficient way of solving the inverse problem in the context of medical electrical impedance tomography. Building upon the current work with the future steps outlined will allow for better recreations and in-person testing when lab space becomes available.